Sometimes things go wrong with a backup job. There are many reasons for this, but that’s not the focus of this blog post. We’re going to show you how to remove lingering Backup checkpoints from a Hyper-V Virtual Machine that where not properly removed after a backup on Windows Server 2012 R2 Hyper-V.

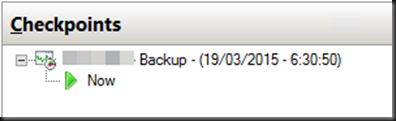
You see checkpoint with a “odd” icon that looks like this

You can right click on the checkpoint but you will not find an option to apply or delete it.This is a recovery snapshot and you’re not supposed to manipulate this manually. It’s there as part of the backup process. You can read more about that in my blog posts Some Insights Into How Windows 2012 R2 Hyper-V Backups Work and What Is AutoRecovery.avhdx all about?.

When we look ad the files we see the traces of a Windows Server 2012R2 Hyper-V backup

Some people turn to manually merging these checkpoints. I have discussed this process in blog posts 3 Ways To Deal With Lingering Hyper-V Checkpoints Formerly Known as Snapshots and Manually Merging Hyper-V Checkpoints. But you don’t have to do this! As a matter of fact you should avoid this if possible at all. The good news is that this can be done via PowerShell.

I’m not convinced the fact that you can’t do it in the GUI is to be considered a bug as some would suggest. The fact is you’re not supposed to have to do this, so the functionality is not there. I guess this is to protect people from trying to delete one by mistake when they see one during backups.

Anyway, PowerShell to the rescue!

So we run:

Get-VMSnapshot -ComputerName "MyHyperVHost" -VMName "VMWithLingeringBackupCheckpoint"

This show us the checkpoint information (note it does not show you the XXX-AutoRecovery.avhdx” as a checkpoint.

And then we simply run Remove-VMSnapshot

#Just remove the lingerging backup checkpoint like you would a normal one via PoSh 
Get-VMSnapshot -ComputerName "MyHyperVHost" -VMName "VMWithLingeringBackupCheckpoint" | Remove-VMSnapshot